Understanding how to find horizontal asymptotes is a key concept in algebra, calculus, and graphing functions. Horizontal asymptotes describe how a function behaves as the input values become extremely large or extremely small. In real terms, they tell us where a graph is “heading” as it stretches infinitely left or right.

Many students struggle with horizontal asymptotes because the rules differ depending on the type of function—whether it’s rational, polynomial, or exponential. This article breaks down the concept in a clear, logical, and beginner-friendly way, backed by mathematical reasoning and real classroom experience.

By the end of this guide, you’ll confidently know how to find horizontal asymptotes of a function, rational functions, and exponential functions, using reliable rules that work every time.

What Are Horizontal Asymptotes?

Horizontal asymptotes are horizontal lines that a graph approaches but may never touch as x approaches positive or negative infinity. They describe the end behavior of a function.

A function can have:
• No horizontal asymptotes
• One horizontal asymptote
• Two different horizontal asymptotes

They are essential in:
• Graphing functions accurately
• Understanding limits
• Solving calculus problems
• Predicting long-term behavior

How to Find Horizontal Asymptotes of a Function

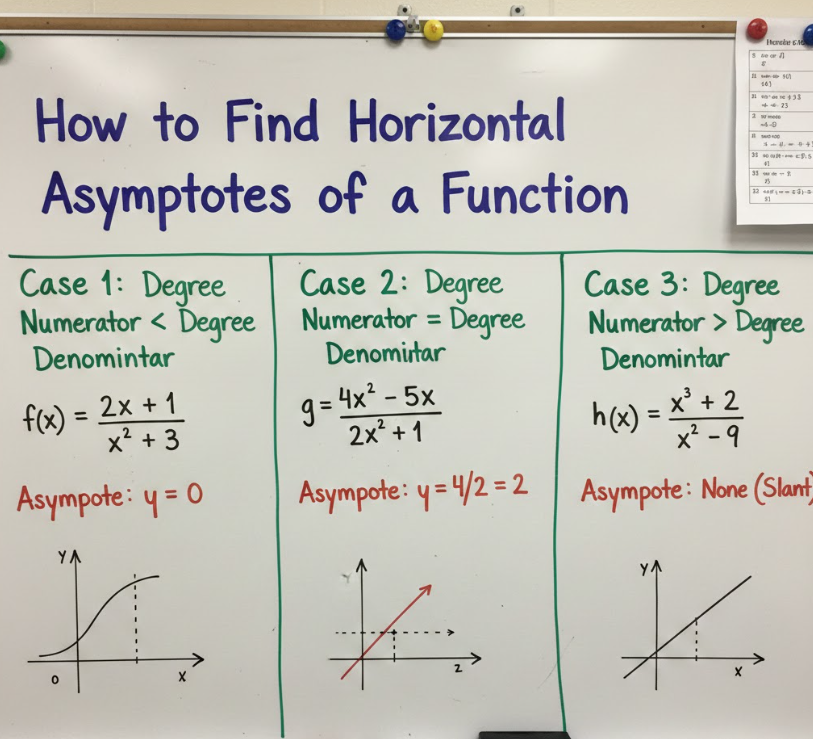
Knowing how to find horizontal asymptotes of a function means understanding what happens to the function as x becomes very large (x → ∞) or very small (x → −∞). Instead of plugging in specific numbers, we analyze the overall structure of the function.

Horizontal asymptotes are closely tied to limits, but you don’t always need advanced calculus to find them. Often, simple comparison of dominant terms gives the correct result.

Key Build Points

• Understand end behavior clearly
Focus on what happens to the function as x increases or decreases without bound. Ignore small terms and focus on dominant ones.

• Identify the type of function first
Polynomial, rational, and exponential functions behave differently. Correct classification simplifies the process.

• Compare growth rates of terms
Terms with higher powers of x grow faster and dominate the function’s behavior.

• Use limits conceptually or formally
Limits help formalize horizontal asymptotes, especially in calculus-based problems.

• Remember asymptotes describe trends, not barriers
Graphs can cross horizontal asymptotes temporarily; this does not invalidate them.

• Confirm visually when graphing
Graphing calculators or software help verify asymptotes but should not replace analytical reasoning.

Also Read:- How to Delete Telegram Account (Step-by-Step Complete Guide)

How to Find Horizontal Asymptotes of Rational Functions

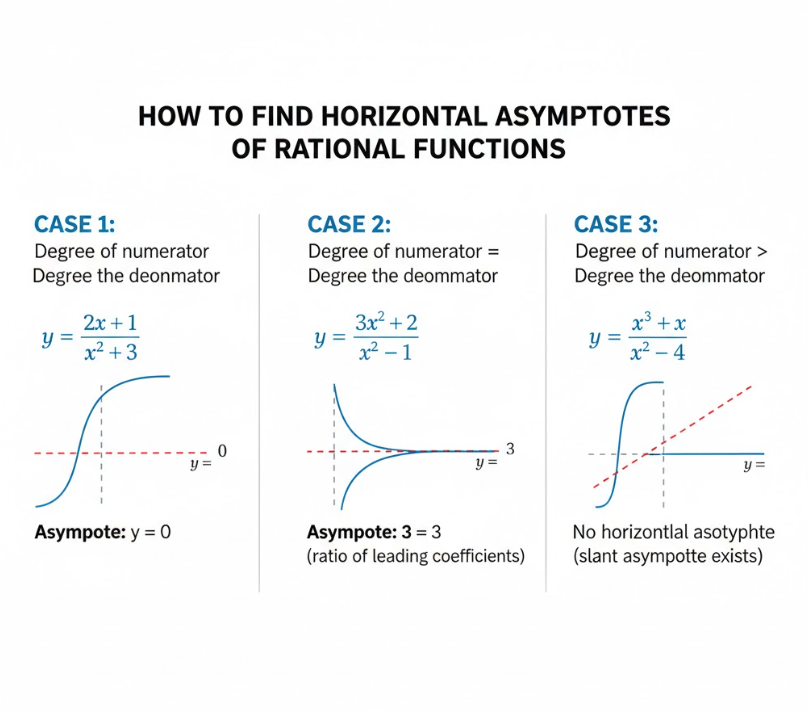
Learning how to find horizontal asymptotes of rational functions is one of the most important graphing skills in algebra and calculus. A rational function is a fraction where both the numerator and denominator are polynomials.

The horizontal asymptote depends entirely on the degrees of the polynomials, not their coefficients alone. This rule-based approach makes rational functions predictable and easier to analyze.

Key Build Points

• Compare degrees of numerator and denominator
The degree is the highest exponent of x in each polynomial.

• Numerator degree < denominator degree
If the numerator’s degree is smaller, the horizontal asymptote is y = 0.

• Numerator degree = denominator degree
Divide the leading coefficients; the ratio gives the horizontal asymptote.

• Numerator degree > denominator degree
There is no horizontal asymptote (but possibly a slant asymptote).

• Ignore lower-degree terms
As x grows large, only the highest-degree terms matter.

• Apply consistently across all rational functions
This method works universally, regardless of complexity.

Also Read:- How to Learn to Code: A Complete Beginner-to-Advanced Roadmap

How to Find Horizontal Asymptotes of a Rational Function (Step-by-Step)

Although similar to the previous topic, how to find horizontal asymptotes of a rational function focuses on applying the rules methodically to a single function. Precision matters here, especially in exams.

This approach emphasizes structure, logic, and verification, helping students avoid common mistakes.

Key Build Points

• Identify leading terms first
Extract the highest-power terms from both numerator and denominator.

• Compare degrees carefully
Even a single-degree difference changes the result completely.

• Simplify coefficients accurately
When degrees match, simplify leading coefficients properly.

• Avoid canceling terms incorrectly
Canceling terms does not affect horizontal asymptotes unless it changes degrees.

• Check behavior at ±∞
Sometimes limits differ for positive and negative infinity.

• Graph to confirm reasoning
Graphs help reinforce analytical results and build confidence.

Also Read:-How to Factory Reset iPhone: Complete Step-by-Step Expert Guide

How to Find Horizontal Asymptotes of Exponential Functions

Understanding how to find horizontal asymptotes of exponential functions requires a different mindset. Exponential functions grow or decay rapidly, and their asymptotes are influenced by constants and transformations.

These functions appear frequently in real-world applications such as population growth, radioactive decay, finance, and physics.

Key Build Points

• Identify the base of the exponential
Bases greater than 1 grow; bases between 0 and 1 decay.

• Look for vertical shifts
Any constant added or subtracted shifts the horizontal asymptote.

• Analyze limits at infinity
Exponential terms often approach zero or infinity.

• Understand natural exponential behavior
Functions like e^x and e^(-x) behave predictably.

• Recognize asymptote location visually
Exponential graphs flatten near their asymptotes.

• Apply transformations consistently
Shifts, reflections, and stretches move asymptotes accordingly.

Also Read:- How to Make Slime: Complete Step-by-Step Guide for Beginners

Common Mistakes Students Make

• Confusing horizontal and vertical asymptotes
• Canceling terms incorrectly
• Ignoring degree comparisons
• Assuming graphs cannot cross asymptotes
• Misinterpreting exponential shifts

Conclusion: Mastering How to Find Horizontal Asymptotes

Learning how to find horizontal asymptotes builds a strong foundation for advanced mathematics. Whether dealing with rational or exponential functions, the rules are logical, consistent, and reliable when applied correctly.

By focusing on dominant terms, degrees, and limits, you can confidently analyze any function’s long-term behavior. This skill is essential for graphing, calculus, and real-world modeling—and once mastered, it makes complex math feel far more manageable.

FAQs:

Q1: Can a function have two horizontal asymptotes?
Yes, when behavior differs as x → ∞ and x → −∞.

Q2: Can a graph cross a horizontal asymptote?
Yes, crossing does not invalidate an asymptote.

Q3: Do all functions have horizontal asymptotes?
No. Many functions have none.

Q4: Are horizontal asymptotes always at y = 0?
No. They depend on function structure and transformations.

For More Updates Visit: Biomagazine