Understanding how to find surface area is a fundamental concept in mathematics, geometry, engineering, architecture, and real-world problem solving. Surface area refers to the total area that covers the outer surface of a three-dimensional object. Whether you’re calculating the amount of paint needed for a wall, determining packaging material, or solving academic problems, learning surface area is essential.
Surface area is measured in square units such as square meters (m²), square centimeters (cm²), or square feet (ft²). It represents the sum of all exposed faces of a solid object. Students, teachers, engineers, designers, and construction professionals frequently use surface area calculations in their work.
This comprehensive guide explains how to find surface area of a rectangular prism, triangular prism, cylinder, and cube using formulas, practical examples, and expert techniques. By the end of this guide, you will clearly understand the formulas, logic, and practical applications behind surface area calculations.
Understanding Surface Area: Definition, Importance, and Core Geometry Concepts

Surface area is the total area of all external faces of a three-dimensional object. Every solid object has an outer boundary, and calculating this boundary area helps determine how much material is needed to cover it.
Surface area calculations are widely used in mathematics, physics, construction, packaging design, and manufacturing industries.
Key concepts involved in understanding surface area:
. Surface area measures the outer coverage of a 3D object
Surface area represents the sum of all visible outer faces of a three-dimensional shape. Every solid object, whether simple or complex, has a boundary that separates it from its surroundings. Calculating this boundary helps measure how much space the object occupies externally.
This concept is different from volume, which measures internal space. Surface area focuses only on the outside part of the object. For example, when painting a box, you calculate surface area, not volume.
Surface area helps determine material requirements such as paint, wrapping paper, insulation, or construction materials.
. Surface area uses square measurement units
Surface area is always expressed in square units such as cm², m², or ft². These units represent two-dimensional measurement of flat surfaces.
Each face of a solid contributes to the total surface area. Adding all face areas provides the total external area.
Using correct units ensures accurate measurement and proper calculation.
. Surface area calculations depend on object shape
Different shapes have different formulas. Cubes, cylinders, prisms, and spheres all require specific formulas.
Understanding shape structure is essential for accurate calculations.
Each face must be identified and measured correctly.
. Surface area helps solve real-world problems
Surface area is used in construction, engineering, and packaging design.
It helps determine material needs and costs.
It also helps improve design efficiency.
. Surface area improves mathematical understanding
Learning surface area improves geometry skills and spatial awareness.
It helps students understand three-dimensional objects better.
This knowledge supports advanced mathematics learning.
. Surface area applies in science and engineering
Surface area affects heat transfer, chemical reactions, and physical properties.
Engineers use surface area to design efficient systems.
Scientists use it in experiments and research.
Also Read:- How to Erase iPhone: Complete Expert Guide for Safe Reset, Trade-In, and Security
How to Find Surface Area of a Rectangular Prism
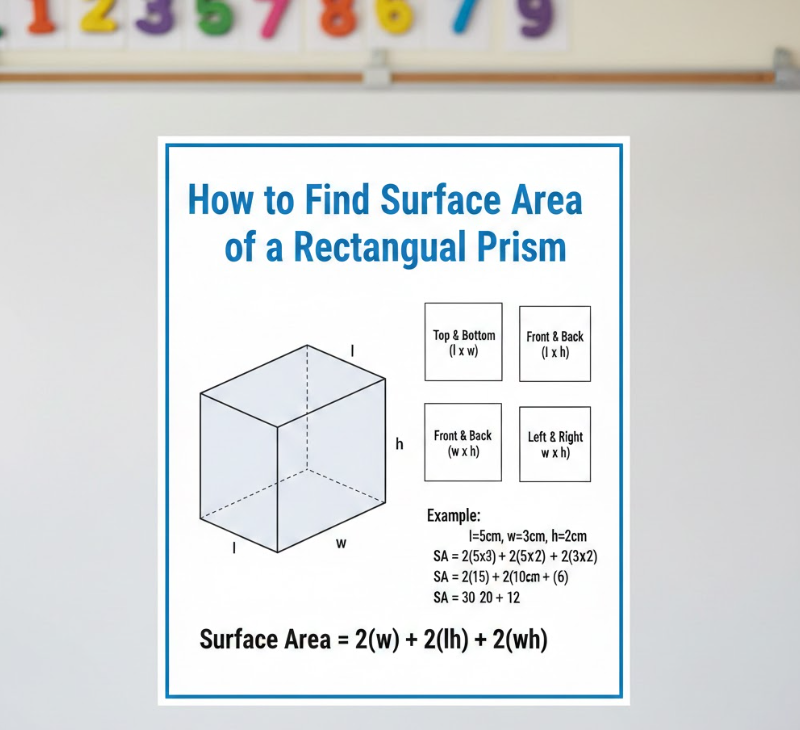
A rectangular prism is a three-dimensional shape with six rectangular faces. Examples include boxes, books, rooms, and storage containers. Understanding how to find surface area of a rectangular prism is essential because this shape appears frequently in real life.
The formula for surface area of a rectangular prism is:
Surface Area = 2(lw + lh + wh)
Where:
l = length
w = width
h = height
Steps to calculate rectangular prism surface area:
. Identify length, width, and height of the prism
The first step in calculating surface area is identifying the three dimensions of the rectangular prism. These dimensions are length, width, and height. Each dimension represents one side of the shape.
You must measure each dimension carefully using appropriate tools such as rulers or measuring tapes. Accurate measurements ensure correct results.
Understanding these dimensions helps identify all six rectangular faces of the prism.
. Calculate area of each rectangular face
Each rectangular prism has three unique face pairs. You calculate area of each using formula:
Area = length × width
Multiply dimensions for each face pair.
This ensures complete surface area coverage.
. Add all face areas together
Add all calculated face areas to get total surface area.
This gives final result.
This represents total external area.
. Use correct square units in answer
Always include square units like cm² or m².
This ensures accurate measurement representation.
Units reflect two-dimensional area.
. Verify calculations for accuracy
Check your calculations to avoid errors.
Accurate calculations ensure correct results.
This improves mathematical accuracy.
Also Read:- How to Use Spirometer: A Complete, Evidence-Based Guide for Safe and Effective Breathing Therapy
How to Find Surface Area of a Triangular Prism
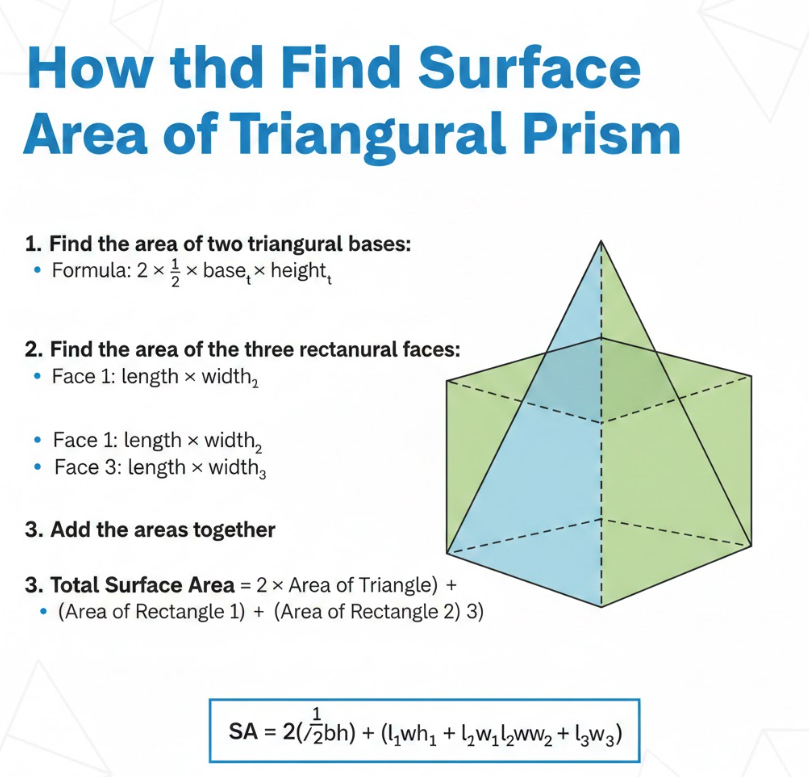
A triangular prism has two triangular bases and three rectangular faces. Understanding how to find surface area of a triangular prism requires calculating both triangular and rectangular faces.
Surface Area Formula:
Surface Area = (2 × Base area) + (Perimeter of triangle × prism length)
Steps to calculate triangular prism surface area:
. Calculate area of triangular base
Use triangle formula:
Area = ½ × base × height
This gives base area.
This represents triangular face area.
This accounts for both ends.
. Find perimeter of triangle
Add all triangle side lengths.
This gives triangle perimeter.
This helps calculate rectangular sides.
. Multiply perimeter by prism length
Multiply triangle perimeter by prism length.
This gives rectangular surface area.
This covers side faces.
. Add all areas together
Add triangle areas and rectangular areas.
This gives total surface area.
This represents full coverage.
. Use proper square units
Include square units in answer.
This ensures accurate representation.
Units reflect area measurement.
Also Read:- How to Use SodaStream: The Complete Expert Guide for Beginners and Advanced Users
How to Find Surface Area of a Cylinder

A cylinder has two circular bases and one curved surface. Understanding how to find surface area of a cylinder is important in engineering, manufacturing, and design.
Formula:
Surface Area = 2πr² + 2πrh
Where:
r = radius
h = height
Steps to calculate cylinder surface area:
. Calculate area of circular bases
Use formula:
Area = πr²
Multiply by two.
This accounts for both bases.
. Calculate curved surface area
Use formula:
Area = 2πrh
This represents curved surface.
This covers side area.
. Add base and curved areas
Add both values together.
This gives total surface area.
This represents complete coverage.
. Use correct radius measurement
Ensure radius is accurate.
Radius affects final result.
Accurate measurement is essential.
. Use π value correctly
Use π = 3.1416.
This ensures accuracy.
This improves precision.
. Include square units in answer
Always include units.
This ensures proper measurement.
Units represent area.
Also Read:- How to Sing: The Complete Expert Guide for Beginners and Advanced Vocalists
How to Find Surface Area of a Cube

A cube has six equal square faces. Understanding how to find surface area of a cube is simple and essential in basic geometry.
Formula:
Surface Area = 6a²
Where a = side length
Steps to calculate cube surface area:
. Measure side length accurately
Measure cube side length.
Accurate measurement ensures correct calculation.
Each face uses same length.
. Calculate area of one square face
Use formula:
Area = side × side
This gives square area.
. Use correct units
Include square units.
This ensures proper measurement.
Units represent area.
. Verify calculation accuracy
Check calculations.
This ensures correct results.
Accuracy is important.
. Apply formula in real problems
Use formula in practical applications.
This improves understanding.
Practice improves skills.
Real-World Applications of Surface Area
Surface area is used in packaging, construction, engineering, and design. It helps calculate materials needed for covering objects.
Examples include painting walls, wrapping boxes, and designing containers.
Surface area improves efficiency and reduces waste.
Also Read:- How to Pop Your Ears: Complete Guide to Safe Ear Pressure Relief
Conclusion
Learning how to find surface area is essential for understanding geometry and solving real-world problems. By using correct formulas and steps, you can calculate surface area of rectangular prisms, triangular prisms, cylinders, and cubes accurately.
Surface area helps in construction, engineering, packaging, and education. With practice and understanding, you can master surface area calculations and apply them confidently in academic and practical situations.
FAQs
What is surface area?
Surface area is total outer area of a 3D object.
Why is surface area important?
It helps calculate material requirements.
Is surface area different from volume?
Yes, surface area measures outside, volume measures inside.
For More Updates Visit: Biomagazine








Leave a Reply